Téléchargez l'archive progdyn.zip qui contient le code à compléter.
Dans de nombreux problèmes, pour trouver la solution, il faut calculer des valeurs pour des sous-problèmes. La "programmation dynamique" est un terme extrèmement mal choisi pour pour désigner les algorithmes où l'on a décelé les sous-problèmes qui sont recalculés inutilement et où l'on réutilise les résultats des calculs déjà effectués.
Il est plus facile de comprendre avec un exemple, prenons en un que beaucoup d'entre vous connaissent, la suite de Fibonacci, dont la définition récursive est la suivante : \[ F_0 = 0, \quad F_1 = 1\] \[ F_{n+2} = F_{n+1} + F_{n} \]
Les valeurs de la suite sont donc : $0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...$
def fibo(n).
Nous vous fournissons une fonction timeit qui va vous permettre de calculer
le temps mis par vos différentes implémentations, son fonctionnement est le suivant :
plutôt que d'appeler une fonction directement, par exemple
f(arg1,arg2,arg3=toto,argblah=blih), vous la
passez en premier argument à timeit et ses arguments ensuite, pour notre exemple
cela donne timeit(f,arg1,arg2,arg3=toto,argblah=blih).
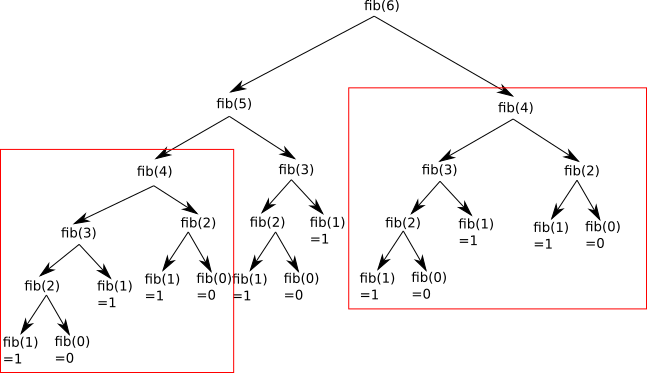
Comme vous pouvez le constater l'execution est relativement lente : elle prend plusieurs
secondes. Cette manière de faire n'est pas efficace car lors du calcul de fibo(n),
fibo(n-1) et fibo(n-2) sont appelées, mais fibo(n-1)
appelle elle-même fibo(n-2) qui est donc recalculée. Vous pouvez voir ci-dessous
l'arbre des appels récursifs (image tirée de pixees.fr) :

Pour éviter cela, on peut commencer par calculer les petites valeurs de la suite et remonter petit à petit vers les plus grandes, de manière à ce que chaque valeur ne soit calculée qu'une seule fois.
def fibo_seq(n) qui calcule $F_n$ en stockant les valeurs
calculées au fur et à mesure dans un tableau. Calculez son temps d'exécution avec timeit,
toujours pour $n=35$.
Reprenons notre implémentation récursive fibo de la fonction de Fibonacci,
idéalement, on souhaiterait pouvoir la conserver telle quelle et trouver un moyen de ne pas
faire les appels récursifs inutiles.
Un moyen de faire ça est d'avoir un dictionnaire dans lequel on stockerait après chaque calcul le résultat de ce calcul.
def memoize(f): qui prend en argument une
fonction f et qui renvoie une nouvelle fonction f_memoizee
construite à partir de f : celle-ci vérifiera si elle a déjà
été appelée avec ces arguments grâce à un
dictionnaire, si c'est le cas, elle utilise le resultat qui y a été stocké, sinon elle appelle
f afin d'effectuer le calcul.
fibo, définie ci-dessous, pour $n=35$ :
fibo = memoize(fibo)
On notera que dans le cas de Fibonacci, la mémoization utilise plus de mémoire que la version la plus "optimisée" de calcul qui ne retient que les deux dernières valeurs calculées : la mémoization retient toutes les valeurs calculées, ce qui n'est pas toujours nécessaire.
Notre première "vraie" application de la programmation dynamique va consister à trouver un algorithme en $O(n^3)$ qui calcule les chemins les plus courts entre tous les sommets d'un graphe ne contenant pas de cycle négatif.
Dans le cas de Fibonacci, on pouvait déduire les sous-problèmes à ne pas recalculer de la relation de récurrence, qui était facile à trouver, étant donné qu'il s'agit de la définition même. En règle générale trouver une relation entre un problème et ses sous-problèmes n'est pas forcément évident, et il faut trouver la "bonne" relation. Il n'y a pas de recette miracle pour trouver celle-ci malheureusement. Celle-ci découle souvent d'une observation sur comment passer d'un problème plus petit à un problème plus grand.
Pour le calcul de tous les chemins les plus courts dans un graphe, nous allons nous baser sur
l'observation suivante : prenons un graphe à $k$ sommets $\{1,\dots,k\}$, et $d^k(i,j)$ le poids
du chemin minimal pour aller de $i$ à $j$ (et $\infty$ sinon). On notera $p_{i,j}$ le poids
de l'arête $(i,j)$ (qui vaudra $\infty$ si elle n'existe pas).
Si on ajoute un sommet $(k+1)$ au graphe et des arêtes de $(k+1)$ vers les autres sommets, alors
il faut recalculer les chemins les plus courts :
Graphe du fichier graphe.py dans la methode tous_plus_courts(self). Cette méthode renverra un tableau bidimensionnel m de taille $n\times n$ contenant en m[i][j]
le poids du plus court chemin de $i$ vers $j$ (ou $\infty$ si $j$ n'est pas accessible à partir
de $i$).
Vous pourrez tester le résultat de votre code en comparant certains poids m[i][j] avec le résultat de pcc(i,j), qui calcule le plus court chemin de $i$ à $j$ avec l'algorithme de Dijkstra. Nous vous avons également fourni une fonction permettant de générer un graphe aléatoire : Graphe.GrapheAleatoire.
On a en entrée un tableau $T$ de $n$ entiers (positifs et négatifs), et on souhaite trouver le
sous-tableau (non-vide) dont la somme des éléments est maximale. Par exemple, si le tableau est
[-2,2,-1,3,-4,1], le plus grand sous tableau est [2,-1,3] dont la somme est 4.
Un algorithme naïf pour trouver le sous-tableau maximal est de parcourir tous les $0\leq i\leq j\lt n$ et de trouver le couple qui définit le sous-tableau de somme maximale. Un tel algorithme aurait une complexité $\mathcal{O}(n^2)$.
Un exemple intéressant et visuel de programmation dynamique est le Seam Carving, une technique de redimensionnement d'images où l'on essaye de conserver les parties intéressantes. Voici un exemple d'image original et d'image redimensionnée en largeur :


Le seam carving peut faire l'objet d'un devoir maison ou TP intéressant.
Un problème que nous rencontrons quasiment tous les jours est celui de la recherche de mots dans un texte. Nous allons voir ici un algorithme très simple qui permet de chercher un (ou plusieurs) mot dans un texte de manière efficace en moyenne.
Pour cela nous allons utiliser une fonction de hachage déroulant : une fonction de hachage qui à partir du hachage d'un mot $w_0\dots w_k$ permette facilement de calculer le hachage du mot $w_1\dots w_{k+1}$. L'idée étant que le hachage a une partie en commun, celle correspondant à $w_1\dots w_k$. Le principe est illustré par la figure suivante (tirée de là) :
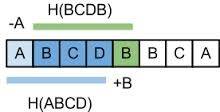
Un exemple de telle fonction peut être le suivant : \[ h(w_0\dots w_k) = \sum_{i=0}^k w_i b^{k-i} \mod p \] où $b$ et $p$ sont des entiers bien choisis (de manière à éviter que trop de collisions), on a alors la relation suivante : \[ h(w_1\dots w_{k+1}) = \left(h(w_0\dots w_k)-b^k w_0\right)\cdot b+w_{k+1} \mod p \]
L'idée de l'algorithme de Rabin-Karp est alors de calculer le hachage du mot que l'on cherche $w$ et de le comparer au hachage des mots à chaque position dans le texte. Si les hachages correspondent, on doit alors comparer les mots pour être sûrs qu'ils sont égaux.
Si la fonction de hachage est bien choisie, les faux positifs sont rares et on fait très peu de comparaisons de mots. Les comparaisons de mots étant coûteuses, contrairement aux comparaisons d'entiers, l'algorithme est en général efficace.
Un autre avantage de cet algorithme est qu'il permet facilement de chercher plus d'un seul mot dans un texte, sans perte d'efficacité.
cherche_mot(mot,texte) du fichier texte.py qui cherche le mot
mot dans le texte texte en utilisant $b=11$ et $p=2^{16}$. Nous vous avons
fourni un exemple de texte et deux mots.